编辑者前言

中国大陆的研究生课程中普遍都包含了宏观经济学课程。不同于本科阶段的宏观经济学，研究生阶段的宏观经济学并不是曼昆甚至高鸿业书中那样，充满大量的文字描述，更多的是千奇百怪的函数和数学模型，你会迷茫到以为翻开了一本数学书。

更要命的是现行的高级宏观经济学教材，目前较为普遍使用的是罗默（David Romer）的《高级宏观经济学》（ ADVANCED MACROECONOMICS），但即使您已经学过难度稍高的宏观经济学教材（例如多恩布什《宏观经济学》），仍然有大量陌生的内容，更不用提书中大量的证明跳步让人根本摸不清头脑。令人难过的是，这本教材甚至不是所有高级宏观经济学教材中难度最高的，难度更高还有的巴罗、Acemoglu、Galí 等人的书，罗默书在这几位的作品中甚至算是难度偏低的。

这份教程试图减少你学习高级宏观经济学的痛苦。首先，这份教程使用的教材为 Campante, F., Sturzenegger, F. and Velasco, A. (2021) Advanced Macroeconomics: An Easy Guide. London: LSE Press. ，这本书有如下优点：

• 采用 CC-4-BY-NC 协议进行许可，你可以 在这里 直接下载到这本书的完整内容。
• 简化了大量符号，避免像罗默书那样大量括号堆积（代价是一定程度上丧失严谨性）。
• 知识密度降低，对知识进行了拆分且进行了更加细节的讲解。

随之带来的缺点也很明显：其模型并不是当前共识的模型，如果你需要使用 Dynare 进行宏观经济学计算，所使用的函数形式并不是这本书中展示的，相关教程使用的也是更复杂的模型与参数。

这份教程对上书的重要部分进行了翻译（注：为了避免不同版本的翻译错误，本书涉及人名的部分不做任何翻译，包括如 Ramsey 模型这样的模型名，但会使用常用的缩写，例如 RBC、DSGE 等），并加入了大量的推导过程和原因解释，即便你没有特别好的数理基础，也可以较为清楚地理解宏观经济学的逻辑和视角。

需要注意的是，如果宏观经济模型是您的学术方向，这份教程是远远不够的，您可能仍然需要学习罗默甚至难度更高的教材。此外，经济学专业也虽没有数学专业那么高的数理能力要求，您仍然需要掌握一定微积分知识（例如如何解微分方程）。

书本前言

Paul Samuelson once stated that “macroeconomics, even with all of our computers and with all of our information is not an exact science and is incapable of being an exact science”. Perhaps this quote captures the view that the feld of macroeconomics, the study of aggregate behaviour of the economy, is full of loose ends and inconsistent statements that make it difcult for economists to agree on anything.

保罗·萨缪尔森曾说过，“宏观经济学，即使有了我们所有的计算机和所有的信息，也不是一门精确的科学，也不可能成为一门精确的科学”。也许这句话概括了这样一种观点，即宏观经济学领域，即对经济总体行为的研究，充满了漏洞和不一致的陈述，使得经济学家很难在任何事情上达成一致。

While there is truth to the fact that there are plenty of disagreements among macroeconomists, we believe such a negative view is unwarranted. Since the birth of macroeconomics as a discipline in the 1930s, in spite of all the uncertainties, inconsistencies, and crises, macroeconomic performance around the world has been strong. More recently, dramatic shocks, such as the Great Financial Crisis or the Covid pandemic, have been managed – not without cost, but with efective damage control. Tere is much to celebrate in the feld of macroeconomics.

尽管宏观经济学家之间存在诸多分歧，但我们认为这种负面观点是没有根据的。自 20 世纪 30 年代宏观经济学作为一门学科诞生以来，尽管存在各种不确定性、不一致性和危机，但世界各地的宏观经济表现一直强劲。最近，诸如全球金融危机或 Covid 疫情等剧烈冲击也得到了控制——虽然并非没有代价，但进行了有效的损害控制。宏观经济学领域有很多值得庆祝的地方。

Macroeconomics was born under the pain of both U.S. and UK’s protracted recession of the 1930s. Until then, economics had dealt with markets, efciency, trade, and incentives, but it was never thought that there was place for a large and systematic breakdown of markets. High and persistent unemployment in the U.S. required a diferent approach.

宏观经济学诞生于 20 世纪 30 年代美国和英国长期衰退的痛苦之中。在此之前，经济学研究的是市场、效率、贸易和激励，但从未有人认为市场会出现大规模和系统性的崩溃。美国持续的高失业率需要一种不同的方法。

The main distinctive feature to be explained was the large disequilibrium in the labour market. How could it be that a massive number of people wanted to work, but could not fnd a job? Tis led to the idea of the possibility of aggregate demand shortfalls – and thus of the potential role for government to prop it up, and, in doing so, restore economic normalcy. “Have people dig a hole and fll them up if necessary” is the of-quoted phrase by Keynes. In modern economic jargon, increase aggregate demand to move the equilibrium of the economy to a higher level of output.

需要解释的主要特点是劳动力市场的大规模失衡。 为什么会有大量的人想工作，却找不到工作？ 这就引出了总需求不足的可能性——以及政府支持总需求，从而恢复经济常态的潜在作用。“让人挖个坑再填上，如有必要”是凯恩斯经常被引用的一句话。 用现代经济术语来说，就是增加总需求，将经济的均衡点转移到更高的产出水平。

Thus, an active approach to fscal and monetary policy developed, entrusting policy makers with the role of moderating the business cycle. Te relationship was enshrined in the so-called Phillips curve, a relationship that suggested a stable tradeof between output and infation. If so, governments simply had to choose their preferred spot on that tradeof.

因此，一种积极的财政和货币政策方法得以发展，赋予政策制定者缓和商业周期的角色。这种关系体现在所谓的菲利普斯曲线中，这种曲线表明产出和通货膨胀之间存在稳定的权衡。如果是这样，政府只需选择他们在该权衡中的首选位置。

Then things changed. Higher infation in the 60s and 70s, challenged the view of a stable tradeof between output and infation. In fact, infation increased with no gain in output, the age of stagfation had arrived. What had changed?

然后事情发生了变化。60 年代和 70 年代更高的通货膨胀挑战了产出和通货膨胀之间稳定权衡的观点。事实上，通货膨胀上升，但产出没有增加，滞胀时代已经到来。什么发生了变化？

Answer had to do with the role of expectations in macroeconomics[1]

答案与预期在宏观经济中的作用有关

Te stable relationship between output and infation required static expectations. People did not expect infation, then the government found it was in its interest to generate a bit of infation – but that meant people were always wrong! As they started anticipating the infation, then its efect on employment faded away, and the efectiveness of macro policy had gone stale.

产出和通胀之间稳定的关系需要静态预期。人们不预期通胀，然后政府发现制造一点通胀符合其利益——但这意味着人们总是错的！当他们开始预期通胀时，它对就业的影响就消失了，宏观政策的有效性也变得陈旧。

Te rational expectations revolution in macroeconomics, initiated in the 1970s, imposed the constraint that a good macro model should allow agents in the model to understand it and act accordingly. Tis was not only a theoretical purism. It was needed to explain what was actually happening in the real world. Te methodological change took hold very quickly and was embraced by the profession. As a working assumption, it is a ubiquitous feature of macroeconomics up to today.

20 世纪 70 年代发起的宏观经济学中的理性预期革命，提出了一个约束条件，即一个好的宏观模型应该允许模型中的行为者理解它并采取相应的行动。这不仅仅是一种理论上的纯粹主义。它需要解释现实世界中实际发生的事情。这种方法论的改变很快被接受，并被该行业所采纳。作为一个工作假设，它至今仍然是宏观经济学中普遍存在的一个特征。

Ten an additional challenge to the world of active macroeconomic policy came about. In the early 1980s, some macroeconomists started the “real business cycles” approach: they studied the neoclassical growth model – that is, a model of optimal capital accumulation – but added to it occasional productivity shocks. Te result was a simulated economy that, they argued, resembled on many dimensions the movements of the business cycle. Tis was a dramatic fnding because it suggested that business cycles could actually be the result of optimal responses by rational economic agents, thereby eschewing the need for a stabilising policy response. What is more, active fscal or monetary policy were not merely inefective, as initially argued by the rational expectations view: they could actually be harmful.

对积极的宏观经济政策而言，又出现了一个额外的挑战。在 20 世纪 80 年代初，一些宏观经济学家开始了“真实商业周期”方法：他们研究了新古典增长模型——即最优资本积累模型——但偶尔会加入生产力冲击。结果是一个模拟经济，他们认为，在许多方面都类似于商业周期的运动。这是一个戏剧性的发现，因为它表明商业周期实际上可能是理性经济主体最优反应的结果，从而避免了对稳定政策反应的需求。更重要的是，正如理性预期观点最初认为的那样，积极的财政或货币政策不仅无效，而且实际上可能是有害的。

This was the state of the discussion when a group of economists tackled the task of building a framework that recovered some of the features of the old Keynesian activism, but in a model with fully rational agents. Tey modelled price formation and introduced market structures that departed from a perfectly competitive allocation. Tey adhered strictly to the assumptions of rational expectations and optimisation, which had the added advantage of allowing for explicit welfare analyses. Tus, the New Keynesian approach was built. It also allowed for shocks, of course, and evolved into what is now known as dynamic stochastic general equilibrium (DSGE) models.

当时讨论的焦点正是在此。一群经济学家致力于构建一个理论框架，以期在完全理性人的模型中，重新拾起旧凯恩斯主义积极干预政策的若干特征。他们对价格形成机制进行建模，并引入了偏离完全竞争配置的市场结构。他们严格遵循理性预期和最优化的假设，这还带来了一个额外的好处，即能够进行明确的福利分析。由此，新凯恩斯主义方法应运而生。当然，该方法也纳入了冲击的考量，并最终发展成为如今广为人知的动态随机一般均衡（DSGE）模型。

Macroeconomic policymaking evolved along those lines. Nowadays, DSGE models are used by any respectable central bank. Furthermore, because this type of model provides fexibility in the degree of price rigidities and market imperfections, it comprises a comprehensive framework nesting the diferent views about how individual markets operate, going all the way from the real business cycle approach to specifcations with ample rigidities.

宏观经济政策的制定沿着这些方向演变。如今，任何一家体面的中央银行都在使用 DSGE 模型。此外，由于这种类型的模型在价格刚性和市场不完善程度上提供了灵活性，因此它构成了一个全面的框架，涵盖了关于个体市场如何运作的不同观点，从实际商业周期方法一直到具有充足刚性的规范。

But the bottom line is that macroeconomics speaks with a common language. While diferences in world views and policy preferences remain, having a common framework is a great achievement. It allows discussions to be framed around the parameters of a model (and whether they match the empirical evidence) – and such discussions can be more productive than those that swirl around the philosophical underpinnings of one’s policy orientations.

但最重要的是，宏观经济学使用一种通用语言。虽然世界观和政策偏好仍然存在差异，但拥有一个共同的框架是一项伟大的成就。它允许围绕模型的参数（以及它们是否与经验证据相符）来构建讨论——而且这种讨论可能比那些围绕一个人的政策导向的哲学基础进行的讨论更有效率。

This book, to a large extent, follows this script, covering the diferent views – and very importantly, the tools needed to speak the language of modern macroeconomic policymaking – in what we believe is an accessible manner. Tat language is that of dynamic policy problems.

本书在很大程度上秉承这一宗旨，旨在阐述各种观点，尤其侧重于理解并掌握现代宏观经济政策制定的语言工具，并力求以平易近人的方式进行解读。这种语言的核心在于动态政策问题。

We start with the Neoclassical Growth Model – a framework to think about capital accumulation through the lens of optimal consumption choices – which constitutes the basic grammar of that language of modern macroeconomics. It also allows us to spend the frst half of the book studying economic growth – arguably the most important issue in macroeconomics, and one that, in recent decades, has taken up as much attention as the topic of business cycles. Te study of growth will take us through the discussion of factor accumulation, productivity growth, the optimality of both the capital stock and the growth rate, and empirical work in trying to understand the proximate and fundamental causes of growth. In that process, we also develop a second canonical model in modern macroeconomics: the overlapping generations model. Tis lets us revisit some of the issues around capital accumulation and long-run growth, as well as study key policy issues, such as the design of pension systems.

我们从新古典增长模型开始——这是一个通过最优消费选择的视角来思考资本积累的框架——它构成了现代宏观经济学语言的基本语法。它还允许我们用本书的前半部分来研究经济增长——这可以说是宏观经济学中最重要的议题，并且在近几十年里，它所受到的关注与商业周期这一主题一样多。对增长的研究将引导我们讨论要素积累、生产率增长、资本存量和增长率的最优性，以及试图理解增长的直接和根本原因的实证研究。在这个过程中，我们还将发展现代宏观经济学中的第二个规范模型：世代交叠模型。这让我们重新审视围绕资本积累和长期增长的一些问题，并研究关键的政策问题，例如养老金制度的设计。

We then move to discuss issues of consumption and investment. Tese are the key macroeconomic aggregates, of course, and their study allows us to explore the power of the dynamic tools we developed in the frst part of the book. Tey also let us introduce the role of uncertainty and expectations, as well as the connections between macroeconomics and fnance.

然后我们转而讨论消费和投资问题。当然，这些是关键的宏观经济总量，通过对它们的研究，我们可以探索我们在本书第一部分中开发的动态工具的力量。它们还让我们介绍了不确定性和预期，以及宏观经济学和金融之间的联系。

Then, in the second half of the book, we turn to the study of business cycle fuctuations, and what policy can and should do about it. We start with the real business cycle approach, as it is based on the neoclassical growth model. Ten we turn to the Keynesian approach, starting from the basic IS-LM model, familiar to anyone with an undergraduate exposure to macroeconomics, but then showing how its modern version emerged: frst, with the challenge of incorporating rational expectations, and then with the fundamentals of the New Keynesian approach. Only then, we present the canonical New Keynesian framework.

然后在本书的后半部分，我们将转向对商业周期波动的研究，以及政策可以而且应该如何应对。我们从实际商业周期方法开始，因为它基于新古典增长模型。然后我们转向凯恩斯主义方法，从基本的 IS-LM 模型开始，任何具有宏观经济学本科背景的人都熟悉它，然后展示它的现代版本是如何出现的：首先，通过纳入理性预期的挑战，然后是新凯恩斯主义方法的基础。只有这样，我们才会介绍规范的新凯恩斯主义框架。

Once we’ve covered all this material, we discuss the scope and efectiveness of fiscal policy. We also go over what optimal fscal policy would look like, as well as some of the reasons for why in practice it departs from those prescriptions. We then move to discuss monetary policy: the relationship between money and prices, the debate on rules vs discretion, and the consensus that arose prior to the 2008 fnancial crisis and the Great Recession. We then cover the post-crisis development of quantitative easing, as well as the constraints imposed by the zero lower bound on nominal interest rates. We fnish of by discussing some current topics that have been infuencing the thinking of policymakers on the fscal and monetary dimensions: secular stagnation, the fscal theory of the price level, and the role of asset-price bubbles and how policy should deal with them.

一旦我们学习完所有这些内容，我们将探讨财政政策的范围和有效性。我们还将分析最优财政政策的形式，并研究在实践中，财政政策为何会偏离这些既定方案的一些原因。随后，我们转而讨论货币政策：货币与价格之间的关系、规则与相机抉择之争，以及2008年金融危机和次贷危机之前形成的共识。此后，我们还将探讨危机后量化宽松的发展，以及名义利率零下限带来的约束。最后，我们将讨论当前影响财政和货币政策决策者思路的一些议题：长期停滞、物价水平的财政理论，以及资产价格泡沫的作用以及政策应如何应对这些泡沫。

As you can see from this whirlwind tour, the book covers a lot of material. Yet, it has a clear methodological structure. We develop the basic tools in the frst part of the book, making clear exactly what we need at each step. All you need is a basic knowledge of calculus, diferential equations, and some linear algebra – and you can consult the mathematical appendix for the basics on the tools we introduce and use in the book. Troughout, we make sure to introduce the tools not for their own sake, but in the context of studying policy-relevant issues and helping develop a framework for thinking about dynamic policy problems. We then study a range of policy issues, using those tools to bring you to the forefront of macroeconomic policy discussions. At the very end, you will also fnd two appendices for those interested in tackling the challenge of running and simulating their own macroeconomic models.

正如你从这次旋风式的浏览中所看到的，本书涵盖了大量内容。然而，它有一个清晰的方法论结构。我们在本书的第一部分开发了基本工具，清楚地说明了我们在每个步骤中需要什么。你只需要具备微积分、微分方程和一些线性代数的基本知识——你可以查阅数学附录，了解我们在书中介绍和使用的工具的基本知识。自始至终，我们确保介绍这些工具不是为了它们本身，而是在研究与政策相关的问题和帮助开发一个思考动态政策问题的框架的背景下。然后，我们研究一系列政策问题，使用这些工具将你带到宏观经济政策讨论的前沿。最后，你还会发现两个附录，供那些有兴趣应对运行和模拟他们自己的宏观经济模型挑战的人使用。

All in all, Samuelson was right that macroeconomics cannot be an exact science. Still, there is a heck of a lot to learn, enjoy and discover – and this, we hope, will help you become an informed participant in exciting macroeconomic policy debates. Enjoy!

总而言之，萨缪尔森认为宏观经济学不可能成为一门精确的科学，他是对的。不过，仍然有很多东西值得学习、享受和发现——我们希望这本书能帮助你成为激动人心的宏观经济政策辩论中一位知情的参与者。祝你愉快！

Note 注意

[1] Surprisingly, the answer came from the most unexpected quarter: the study of agricultural markets. As early as 1960 John Muth was studying the cobweb model, a standard model in agricultural economics. In this model the farmers look at the harvest price to decide how much they plant, but then this provides a supply the following year which is inconsistent with this price. For example a bad harvest implies a high price, a high price implies lots of planting, a big harvest next year and thus a low price! Te low price motivates less planting, but then the small harvest leads to a high price the following year! In this model, farmers were systematically wrong, and kept being wrong all the time. Tis is nonsense, argued Muth. Not only should they learn, they know the market and they should plant the equilibrium price, namely the price that induces the amount of planting that implies that next year that will be the price. Tere are no cycles, no mistakes, the market equilibrium holds from day one! Transferred to macroeconomic policy, something similar was happening.

令人惊讶的是，答案来自最意想不到的方面：农业市场研究。早在 1960 年，John Muth 就在研究蛛网模型，这是农业经济学中的一个标准模型。在这个模型中，农民根据收获价格来决定种植多少，但这会在第二年提供与该价格不一致的供应。例如，歉收意味着高价，高价意味着大量种植，明年大丰收，因此价格低廉！低价促使减少种植，但随后的小丰收导致第二年价格高涨！在这个模型中，农民系统性地犯错，并且一直犯错。Muth 认为这是胡说八道。他们不仅应该学习，而且应该了解市场，并且应该种植均衡价格，即诱导种植量的价格，这意味着明年这将是该价格。没有周期，没有错误，市场均衡从第一天开始就成立！转移到宏观经济政策，类似的事情正在发生。

经济增长与 Solow 模型

The Kaldor Facts

现代经济增长研究始于战后时期，其研究动机主要源于发达国家的发展经验。Nicolas Kaldor 在其经典论文（Kaldor 1957）中阐述了经济增长普遍遵循的基本规律——至少在当时那些发达国家如此。这些规律后被学界称为 the Kaldor facts，而早期建构的增长理论面临的核心挑战，便是如何同时解释所有这些现象。那么，卡尔多事实究竟包含哪些内容？具体归纳如下：

• 工人人均产出持续增长，且无下滑趋势
• 资本/产出比率基本保持恒定（但需明确资本范畴）
• 工人人均资本量呈持续增长趋势
• 资本回报率保持长期稳定
• 资本要素和劳动要素在国民收入中的份额相对稳定
• 各国工人人均产出增长率存在显着差异（若考虑时间维度，可观察到经济奇迹和衰退周 期并存的现象）

正如 Robert Solow 建立的一个简单模型（Solow 1956）所示，该模型成为经济增长理论的首个实用模型。Solow 的贡献奠定了新古典增长模型（NGM）的基础，正是现代增长理论的基石，因其似乎契合卡尔多事实。任何经济增长研究都必须从该模型入手，既要审视它所能解释的经济现象——显然更重要的是，厘清其无法阐释的理论盲区。

Solow 模型

生产函数 $Y=F(K,L,t)$

其中 $Y$ 为产出，可以被消费（$C$）或投资（$I$）以创造新的实物资本单位。

$s$ 为被保存的产出比例，$1-s$为被消费的产出比例，$0⩽s⩽1$

$\delta$为折旧率，以此可计算某一时间点实物资本存量的增量：

$$\dot{K}=I-\delta \cdot K=s\cdot F\left(K,L,t\right)-\delta \cdot K$$ 其中$\dot{K}$表示对时间的微分。

假设人口就是劳动力$L$，它以恒定的外生速率$n=\frac{\dot{L}}{L}\ge 0$增长，若 $t=0$ 时人口归化为1，那么$t$时的人口$L_t=e^{nt}$

（新古典）生产函数

忽略技术进步，即假设$F(\cdot )$与$t$无关，此时 $Y=F(K,L)$。若一个生产函数的具体形式满足以下三个假设，则可被称之为新古典生产函数：

假设一

对于所有 $K>0$和$L>0$，$F(\cdot )$ 输出的边际产量为正且递减，即： $$\frac{\partial F}{\partial K}>0\frac{\partial F}{\partial L}>0\text{（边际产量为正）}\frac{{\partial }^{2}F}{\partial K^2}<0\frac{{\partial }^{2}F}{\partial L^2}<0\text{（边际产量递减）}$$

假设二

规模报酬不变（Constant returns to scale，CRS） $$\text{For all }\lambda >0,F(\lambda K,\lambda L)=\lambda F(K,L)$$

假设二的存在，可以使得生产函数被表示为 $$Y=F(K,L)=L\cdot F(\frac{K}{L},1)=L\cdot f(k)$$ 其中$k\equiv \frac{K}{L}$，即资本/劳动比率。此时生产函数可被写为$L\cdot F(k,1)$即$L\cdot f(k)$，即可定义生产函数的人均形式$y=f(k)$。

假设三（稻田条件）

资本（或劳动力）投入趋于 0 时，其边际产量趋近于无穷大；而当资本（或劳动力）投入趋于无穷大时，其边际产量趋近于 0。 $$\underset{K\to 0}{\lim }\frac{\partial F}{\partial K}=\underset{L\to 0}{\lim }\frac{\partial F}{\partial L}=\infty \underset{K\to \infty }{\lim }\frac{\partial F}{\partial K}=\underset{L\to \infty }{\lim }\frac{\partial F}{\partial L}=0$$

科布·道格拉斯函数（下简称 CD 函数）满足上述三个条件，就是一个新古典生产函数，其形式为: $$Y=A{K}^{\alpha }{L}^{1-\alpha }$$ $A>0$ 为技术水平，人均生产函数为 $A{k}^{\alpha }$

资本运动定律

将某一时刻资本存量两边同除$L$：

$$\begin{array}{rl}\dot{K}=& s\cdot F\left(K,L\right)-\delta K\\ \frac{\dot{K}}{L}\left(\text{人均资本量}\right)=& s\cdot f\left(k\right)\text{（人均产出）}-\delta k\end{array}$$

现已定义$k\equiv \frac{K}{L}$，对其在时间上进行微分： $$\dot{k}\equiv \frac{d\left(\frac{K}{L}\right)}{dt}=\frac{\dot{K}L-K\dot{L}}{L^2}=\frac{\dot{K}}{L}-\frac{K}{L}\cdot \frac{\dot{L}}{L}=\frac{\dot{K}}{L}-nk$$

其中，$n=\frac{\dot{L}}{L}$为人口增长率。移项可得： $$\frac{\dot{K}}{L}=\dot{k}+nk$$ 代入最上面式子的左侧并移项： $$\dot{k}=s\cdot f(k)-(\delta +n)k$$ $(\delta +n)$在 式右侧可以被视为资本 / 劳动比率的有效折旧率。如果储蓄率$s$为 0，那么 $k$ 的下降可能是因为$K$的折旧率$\delta$上升，也有可能是因为$L$的增长率$n$上升。

（补充罗默书说明）

这是 Solow 模型的关键方程，它表明了单位有效劳动平均资本存量的变化率是以下两项之差：

• 第一项是$sf(k)$，由于单位有效劳动的平均产出是$f(k)$， 其中用于投资的比例是$s$，因此这一项即为单位有效劳动的实际投资
• 第二项是 $(n+\delta )k$，也叫持平投资，它代表了使得$k$保持在现有水平所需要的投资量。

为了防止$k$不断减少，追加一定数量的投资是必要的，其理由有两点：

• 一是现有资本会折旧，折旧的这部分资本必须得到补偿才能防止资本存量下降，这就是$\delta k$项

• 二是有效劳动的数量在增加，因此仅仅保持资本存量$K$不变的投资（即补偿折旧的投资）并不足以保持单位有效劳动的平均资本存量$k$不变。实际上，由于有效劳动数量的增长率为$n$，资本存量的增长率也必须是$n$才能保持$k$不变，就是$nk$项。

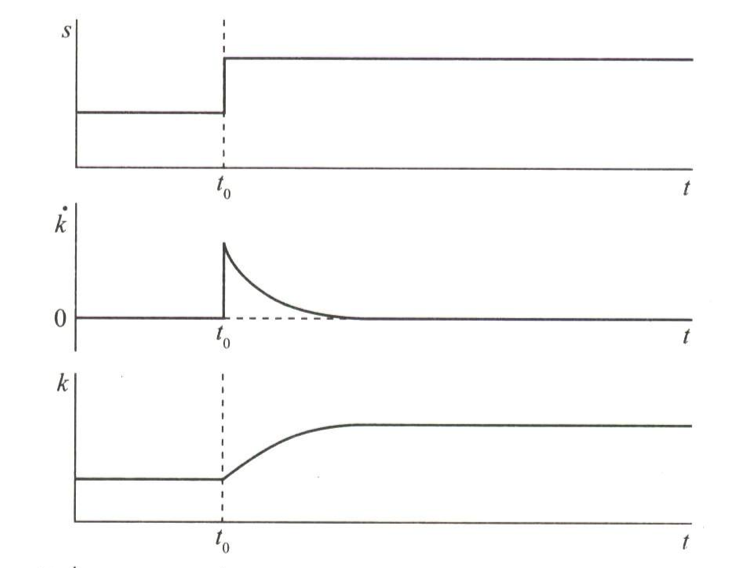
下图说明了这一变化的作用：

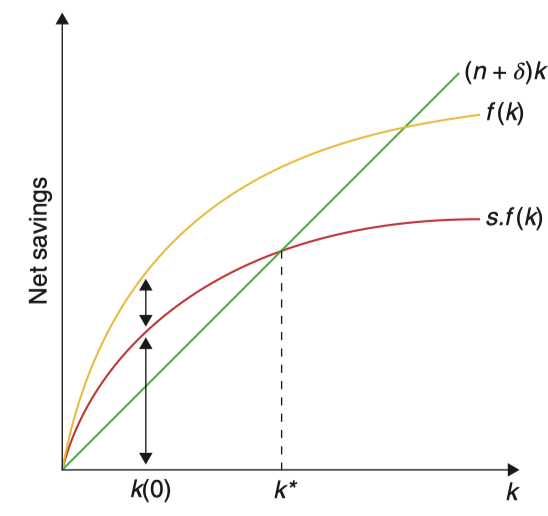
平衡增长路径

平衡增长路径（balanced growth path，以下简称 BGP）指的是各种量以恒定速率增长的情况。

在 Solow 模型中，BGP 对应为 $\dot{k}=0$，对应值为 $k^{\ast }$，满足： $$sf(k^{\ast })=(n+\delta )k^{\ast }$$ 在BGP中，资本劳动比$k$保持恒定，人均产出$k$和人均消费$c$稳定在$y^{\ast }=f(k^{\ast })$和$c^{\ast }=(1-s)f(k^{\ast })$的水平。

现代入CD函数$f(k)=A{k}^{\alpha }$，可得BGP中 $$k^{\ast }={\left(\frac{sA}{n+\delta }\right)}^{\frac{1}{1-\alpha }}=A^{\frac{1}{1-\alpha }}{\left(\frac{s}{n+\delta }\right)}^{\frac{\alpha }{1-\alpha }}(0<\alpha <1)$$ 这里可以看到，$k^{\ast }$随$s$和$A$的上升而上升，随$n$和$\delta$的下降而下降。

过渡动态

此外，Solow 模型在向 BGP 过渡的过程中也实现了增长

$$\dot{k}=sf(k)-(n+\delta )k$$

现令${\gamma }_k\equiv \frac{\dot{k}}{k}$，则有

$${\gamma }_k=\frac{sf(k)}{k}-(n+\delta )$$

在没到达BGP前，$\frac{sf(k)}{k}$是一个单调递减的函数，而$n+\delta$是一条水平直线，可以推论出BGP时的$k^{\ast }>0$存在且唯一。

进行微分：

$$\frac{d\dot{k}}{dk}=s\cdot f^{\prime }\left(k\right)-\left(n+\delta \right)$$

现代入BGP状态下的$k^{\ast }$，可以看到 BGP 点两边时的收敛趋势：

$${\frac{d\dot{k}}{dk}|}_{k=k^{\ast }}=s\cdot f^{\prime }\left(k^{\ast }\right)-\left(n+\delta \right)$$

可以看到，当满足（A）当$k<k^{\ast }$时$\dot{k}>0$和（B）当$k>k^{\ast }$时$\dot{k}<0$，资本存量$k^{\ast }$会收敛至 BGP，此时${\frac{d\dot{k}}{dk}|}_{k=k^{\ast }}<0$。

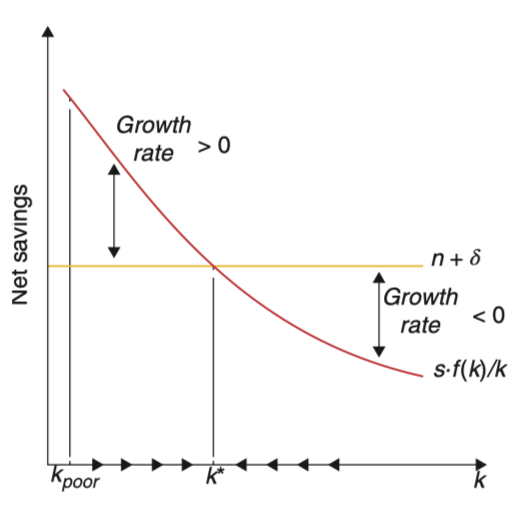
在 CD 函数条件下，这相当于 $${\frac{d\dot{k}}{dk}|}_{k=k^{\ast }}=s\cdot A\alpha {\left(\frac{sA}{n+\delta }\right)}^{-1}-(n+\delta )=(n+\delta )\left(\alpha -1\right)$$

若要满足${\frac{d\dot{k}}{dk}|}_{k=k^{\ast }}<0$，则需要$\alpha <1$——这意味着达到BGP的条件是边际收益递减。

边际收益递减意味着，如果人均资本$k$比较小，那么其边际产出$f^{\prime }(k)$相对较高。根据假设，储蓄率$s$恒定，因此人均资本$k$比较小时，投资储蓄的边际汇报$s{f}^{\prime }(k)$相对较高。又已知人均资本$k$以恒定的速率$n+\delta$进行折旧，因此此时资本增长$\dot{k}$也比较高。总而言之，$k<k^{\ast }$时，人均资本增长$\dot{k}$为正；$k>k^{\ast }$时，人均资本增长$\dot{k}$为负。

政策实验

初始状态下，假设经济处于$k_1^{\ast }$的BGP中，随后某项政策使得储蓄率$s$上升，那么$\frac{sf(k)}{k}$向右移动，新的BGP资本存量$k_2^{\ast }>k_1^{\ast }$。

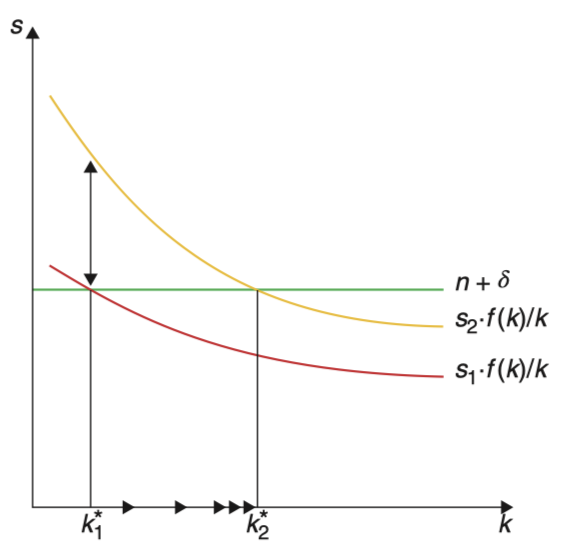
短期内，人均增长率上升，长期来看，技术的永久性提升会带来更高的$k,y$但人均增长率不会变化。

（补充罗默书）

$s$的增加会使实际投资曲线向上移动，从而使$k^{\ast }$上升，如图所示，但$k$的这种变化并不是瞬间实现的。一开始，$k$仍然等于原来的$k$值，但在这一水平上，实际投资是超过持平投资的，即用于投资的资源多于维持$k$不变所需的水平，因此$k$为正数，$k$会开始上涨并一直上涨到新的$\dot{k}$值，此后$k$会在这个新的$k^{\ast }$值上保持不变。

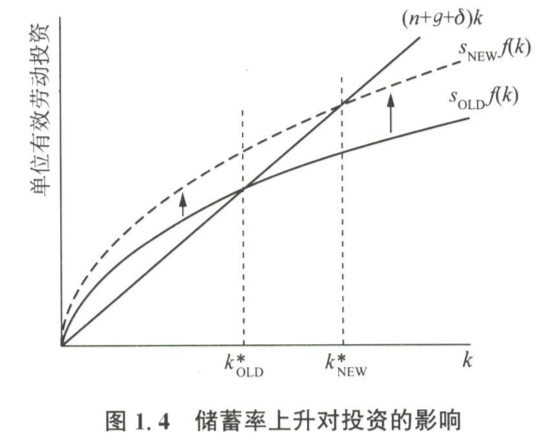
下图中的前三幅小图即描绘了上述结论。$t_0$表示储蓄率出现增加的时刻， 根据假设，$s$在时刻$t_0$突然上升并在此后保持不变。$s$的突然增加使实际投资严格大于持平投资，因此$\dot{k}$将从0跳跃至一个严格为正的值，而$k$则从原来的$k^{\ast }$值逐渐上升至新的$k^{\ast }$值，与此同时$\dot{k}$也随之逐渐回到零值。

动态无效性

已知 $$s\cdot f(k^{\ast })=(n+\delta )k^{\ast }$$

又

$$c^{\ast }=(1-s)f[k^{\ast }(s)]$$

因此 $$c^{\ast }(s)=f[k^{\ast }(s)]-(n+\delta )k^{\ast }$$

对储蓄率求偏导 $$\frac{\partial c^{\ast }\left(s\right)}{\partial s}=\frac{\partial c^{\ast }\left(s\right)}{\partial k^{\ast }}\cdot \frac{\partial k^{\ast }(s)}{\partial s}=\left[f^{\prime }\left(k^{\ast }\right)-\left(n+\delta \right)\right]\cdot \frac{\partial k^{\ast }(s)}{\partial s}\text{\hspace{1em}(1.7.1)}$$

在(1.7.1)中，$k^{\ast }(s)$表示，每个$s$对应一个BGP状态下的$k^{\ast }$，已知储蓄率高的状态下人均资本量也高，因此可得$\frac{d{k}^{\ast }(s)}{ds}>0$。

因此若想让$c^{\ast }(s)$水平最高，条件为$f^{\prime }(k)=n+\delta$，此时的消费率称为黄金法则下的消费率(the “golden rule” consumption rate)：$c_g=f(k_g)-(n+\delta )k_g$

此外，$[f^{\prime }\left(k^{\ast }\right)-\left(n+\delta \right)]$的正负取决于决定$k^{\ast }$的$s$，同样已知储蓄率高的状态下人均资本量也高，那么这意味着最佳消费水平$c^{\ast }$在$s$低水平时随$s$增加而增加，在$s$低水平时随$s$增加而减少。

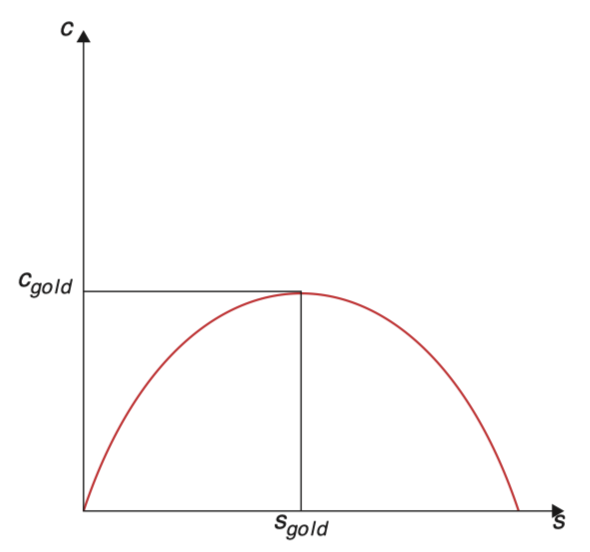
这里可以得出的结论是：若实际储蓄率高于$s_g$，那么经济体仍然可以在 BGP 或在向 BGP 转型的时期提升消费。即当资本存量过高时，资本的边际产出低于储蓄率，导致过度的资本积累，这就是动态无效性。

绝对收敛和条件收敛

回看方程 $${\gamma }_k=\frac{sf(k)}{k}-(n+\delta )$$

现对$k$求偏导，可得

$$\frac{\partial {\gamma }_k}{\partial k}=\frac{s}{k}\left[f^{\prime }\left(k\right)-\frac{f\left(k\right)}{k}\right]<0$$

在其他条件相同的情况下，较小的$k$值与较大的${\gamma }_k$值相关联。 这个结果是否意味着人均资本较低的经济体往往人均增长更快？经济体之间是否存在趋同？

条件收敛：若经济体在结构上有相似性（$s,n,\delta$值相同，$F(\cdot )$形式一致），则它们达到 BGP 时的$k^{\ast },y^{\ast }$均相同，唯一的增长差异来自于初始值$k(0)$。那么可以得出，发展水平较低（具有较低$y(0)$和$k(0)$水平）的经济体会有更高的增长率，最终与富裕经济体趋同。

绝对收敛：较贫穷的国家在不考虑经济其他特征的情况下会增长得更快。

是否可以解释收入差异？

前面已经得到，CD 函数条件下的的 BGP 为： $$k^{\ast }={\left(\frac{sA}{n+\delta }\right)}^{\frac{1}{1-\alpha }}=A^{\frac{1}{1-\alpha }}{\left(\frac{s}{n+\delta }\right)}^{\frac{\alpha }{1-\alpha }}(0<\alpha <1)$$

现令$A=1,n=0$ $$y^{\ast }={\left(\frac{s}{\delta }\right)}^{\frac{\alpha }{1-\alpha }}$$ Solow 模型是否能解释BGP状态下收入差异的能力取决于$\alpha$的值 $$\mathrm{If}\{\begin{array}{ll}\alpha =\frac{1}{3}\mathrm{then}\frac{\alpha }{1-\alpha }=\frac{1/3}{2/3}=\frac{1}{2}& \\ \alpha =\frac{1}{2}\mathrm{then}\frac{\alpha }{1-\alpha }=\frac{1/2}{1/2}=1& \\ \alpha =\frac{2}{3}\mathrm{then}\frac{\alpha }{1-\alpha }=\frac{2/3}{1/3}=2& \end{array}$$ 资本份额的标准（粗略）估值为1/3。然而Parente与Prescott(2002)提出，由于存在大量无形资本资产，GDP中的资本份额远超常规测算值。事实上，他们认为GDP中的投资占比应接近三分之二，而非传统认知的三分之一。未计入投资的成因包括（他们的具体估算数据分别为）：

1. 设备维修保养（占GDP的5%）
2. 研发支出（占GDP的3%）乘以三倍（即GDP的9%）——用于核算生产工艺改进及新产品推出成本（这个「三倍」缺乏充分依据）
3. 软件投资（占GDP的3%）
4. 企业组织资本投入（他们认为12%是合理估值）
5. 在职学习与培训（占GDP的10%）
6. 学校教育支出（占GDP的5%）

他们声称所有这些资本都有回报，约占 GDP 总量的 56%。使用上述方程可以用它来估计收入水平差异。

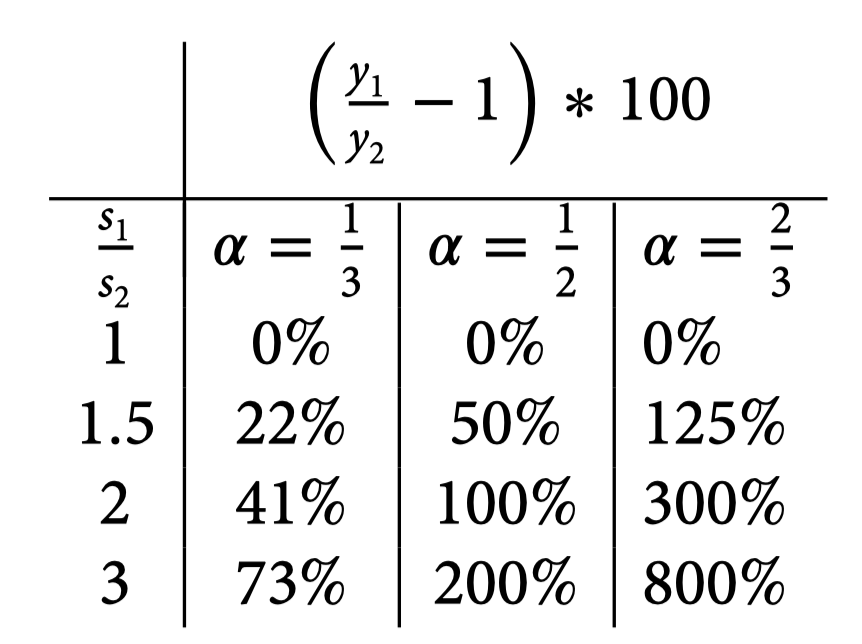
即使使用三分之二估计得到的 800%，相对于我们在数据中看到的情况来说，似乎还是太低了。

另有一种可能：收入差异可能来自全要素生产率（ TFP ）的差异，如参数 $A$ 所捕捉的那样。问题是：这些差异需要多大才能解释产出差异？

因此，如果 $\alpha =2∕3$，如 Parente 和 Prescott （ 2002 ）理论，那么 $$A^{\frac{1}{1-\alpha }}=A^{\frac{1}{1-2/3}}=A^3$$ 这意味着，如果某国 TFP 是即另一国1/3的水平，这表明收入水平则为该国的 1 ∕ 27。

外生技术增长的 Solow 模型

现允许要素生产率随时间变化，在 CD 函数中，这意味着 $A$ 随时间增加。设$\frac{\dot{A}}{A}=a>0$，在还未达到 BGP 时： $$\frac{\dot{y}}{y}=\frac{\dot{y}}{y}+\alpha \cdot \frac{\dot{k}}{k}=a+\alpha \cdot {\gamma }_k$$

在 BGP 时，$k$为常数，此时 $$\frac{\dot{y}}{y}=a$$

结论：从长远来看，技术进步是人均收入增长的唯一来源。

先将技术进步融入劳工：$L$不仅仅为劳动人口，而是人力资本，定义： $$E_t=L_t\cdot e^{\lambda t}=L_0\cdot e^{(\lambda +n)t}$$

此时生产函数为 $Y=F(K_t,E_t)$。从人均效率角度看，可以定义$k=\frac{K}{E}$，那么$\dot{k}=\frac{\dot{K}E-K\dot{E}}{E^2}$，此时 $$\begin{array}{rl}\frac{\dot{k}}{k}& =\frac{\dot{K}E-K\dot{E}}{E^2}\cdot \frac{E}{K}\\ & =\frac{\dot{K}E-K\dot{E}}{KE}=\frac{\dot{K}}{K}-\frac{\dot{E}}{E}\end{array}$$

已知${\gamma }_k=\frac{\dot{k}}{k}=\frac{sf(k)}{k}-(n+\delta )$，所以代入可得 $$\frac{\dot{k}}{k}=\frac{sf(k)}{k}-\delta -n-\lambda$$

两侧乘以$k$得 $$\dot{k}=sf(k)-(\delta +n+\lambda )k$$

当$\dot{k}=0$时，$\frac{sf(k)}{k}=(\delta +n+\lambda )$

$\dot{k}=0$时，处于BGP，因此 $$\frac{\dot{K}}{K}=\frac{\dot{E}}{E}=n+\lambda =\frac{\dot{Y}}{Y}$$

长期来看 $$\frac{\dot{\left(\frac{Y}{L}\right)}}{\frac{Y}{L}}=\frac{\dot{Y}}{Y}-\frac{\dot{L}}{L}=\lambda$$ （因为$\frac{\dot{Y}}{Y}=\lambda +n,\frac{\dot{L}}{L}=n$）

学到了什么？

Solow 模型表明:

• 仅靠资本积累本身无法维持长期人均收入持续增长，因为会受到边际收益递减的制约。
• 若引入技术变革，虽能解释长期增长，但未揭示内在动因。

事实上任何长期增长率差异源于外生给定的技术进步差异，Solow 模型无法解释这些差异的根源，因此无法说明政策对长期增长的作用机制。

话虽如此，我们的确在向长期过渡的过程中，了解到许多关于增长的见解，关于收入水平的差异，以及政策如何影响这些问题。其中有几点重要的启示：（i）收敛——该模型预测有条件收敛；（ii）动态无效率——在这个模型里，可能会出现储蓄过多的情况；（iii）长期收入差异——这些差异似乎与生产力差异息息相关。

动态最优化基础

这是临时决定插入的一个章节，实际上后面一章 Ramsey 模型的内容已经准备完毕，但它总给我一种奇怪的感觉：我不知道为什么这样做是有用的，也不知道为什么最终需要得到这一结果

后来才意识到，Ramsey 模型的推导实际上就是动态最优化（Dynamic Optimization）的思想，而这几乎是一门单独的学科，是经济学与数学的一个交汇处。理解动态最优化思想对后面各种模型的推导非常重要，这应该也是当今国内大学教育缺失的一部分——至少我在本科和研究生阶段都没接触到。

Solow 模型在初级宏观经济学就有出现，因此难度还不算太高（即使最开始对于时间的微分确实涉及到了动态最优化问题），但是如果没有动态最优化的基础，到了 Ramsey 模型你会发现知识似乎出现了极大的跳跃，因此特开辟此章节进行承上启下。

参考：

• B 站：太白金星V博士
• YouTube @PengTitus
• 蒋中一（Alpha C. Ciang）《动态最优化基础》（Elements of Dynamic Optimization）

动态最优化的性质

何为「动态」？

让我们先弄清楚什么是静态问题。某一时刻一家企业的利润函数为 $\pi (x)=F_x(Q)$。现需要求企业最大利润时的产量，很显然方法是求一阶导并令其为0。

通常来说该问题只有一个解，因为这只是在某一时刻下的选择。如果问题的解只是由每个选择变量的单个最优值组成的，这实际上就是静态优化问题。

而动态最优化涉及的问题通常为在计划期间的每个时段（离散时间情形）上或给定时间区间⽐如 $[0，T]$中的每个时点上，选择变量的最优值是多少。也就是说对于每个选择变量，你要给出它在今天的最优值、明天的最优值……直⾄计划期结束时的最优值。

最速曲线问题

在基础数学中，「两点之间线段最短」是一个非常基础的常识，但在物理学中却不尽然。

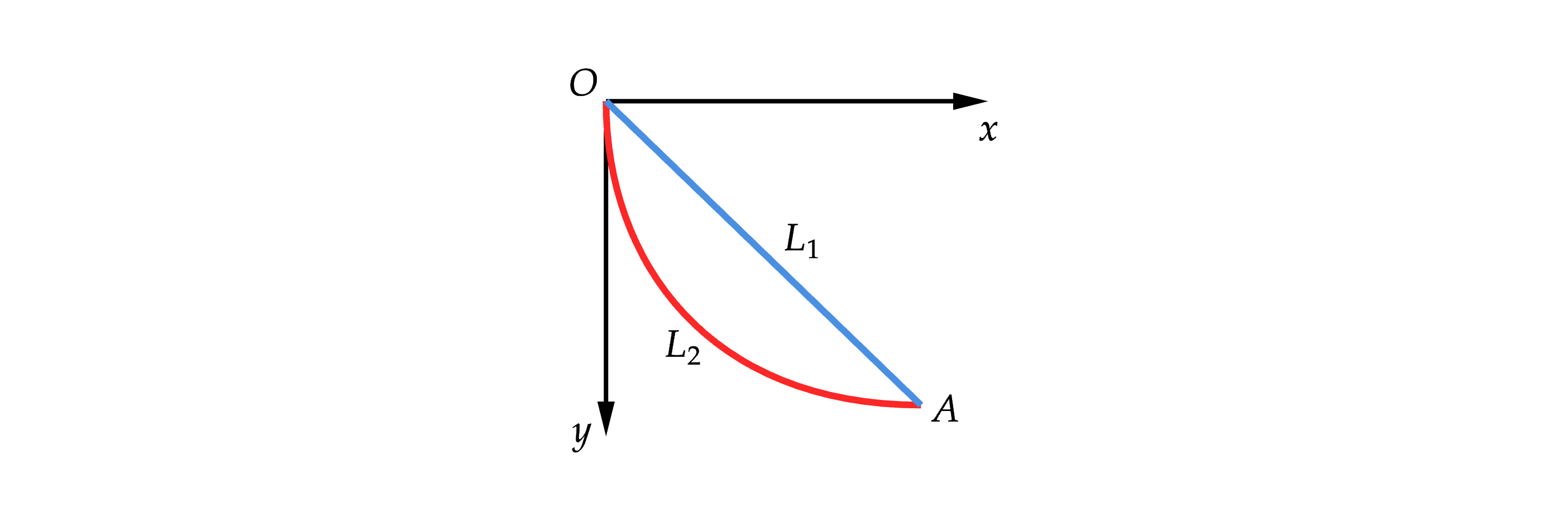
如上图，一个物体从 O 移动到 A 点，在数学几何意义上$L_1$是最短距离，但这并不意味着速度最快，实际上存在另一条路径$L_2$，沿着$L_2$从 O 移动到 A 点的用时最短。我们暂时不关心$L_2$具体的解，而是先看看求解的思考过程。

根据机械能守恒定理，满足 $$mgy=\frac{1}{2}m{v}^2$$ 其中$mgy$是重力势能，$\frac{1}{2}m{v}^2$为动能。由此可以解出 $$v=\sqrt{2gy}$$ 假设在某一时刻物体经过的路线长度为$s$，根据勾股定理有 $$ds=\sqrt{d{x}^2+d{y}^2}=dx\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}$$ 某一点的速度等于路程除以时间，那么就有 $$v=\frac{ds}{dt}⟹dt=\frac{ds}{v}$$ 两边同时积分，$dt$的积分即为在整段从 O 移动到 A 点所用的时间，令其为$T$，右边改为对 $x$ 积分。 $$\begin{array}{rl}\int dt=& \int \frac{ds}{v}\\ T=& \int \frac{\sqrt{d{x}^2+d{y}^2}}{\sqrt{2gy}}\\ T=& \int \frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}{\sqrt{2gy}}dx\end{array}$$ 要想求出最快的运动路径，实际就是让$T$最小。但需要注意的是，我们需要求的是「路径」，而不是一个「点」，而「路径」本身其实又是一个函数。我们知道，函数是一种从一个值映射到另一个值，而这里的 $T$ 却是从一个函数映射到另一个值。

这就是它的特别之处，一种路径到值的映射，这类映射有一个特别的名字：泛函（Functional）。接下来关于动态最优化的一个重要方法——变分法（Calculus of variations），其起点就是这里的泛函。

预备定理

在进入变分法前需要先了解下面这个定理，这个定理非常直观，很好理解，这里也会给出非常简洁的代数证明。

定理

对于函数$M(x)$ 和任意满足$h(a)=h(b)=0$的函数 $h(x)$ ，若有 $${\int }_a^{b}M\left(x\right)h\left(x\right)dx=0$$ 那么 $$M(x)=0$$

证明

令$h(x)=-M(x)(x-a)(x-b)$，其满足$h(a)=h(b)=0$。

代入得 $${\int }_a^{b}M\left(x\right)h\left(x\right)dx={\int }_a^{b}M\left(x\right)\cdot -M(x)(x-a)(x-b))={\int }_a^b{M}^2(x)(-(x-a)(x-b))dx=0$$ 易知在$(a,b)$区间$-(x-a)(x-b)>0$，若要使得该式成立，那么一定有$M^2(x)=0$，所以可以得到 $$M(x)=0$$

变分法的思想

回到前面的问题：

虽然我们暂时无法得知最佳路径$L_2$的具体表达，但我们至少可以知道这条曲线本身是存在的，我们记为$y^{\ast }$，而我们的目的，则是在众多的可能的$y$路径中找到这个最优路径。我们可以这样表示一条与最佳路径相邻的，同样可以从 O 运动到 A 的可能路径： $$y(x)=y^{\ast }(x)+\epsilon \eta (x)$$ 其中，$\epsilon$是一个常数，$\eta (x)$是一条路径，因为其同样可以从 O 运动到 A ，所以满足$\eta (0)=\eta (T)=0$。此外，$\eta (x)$ 必须是平滑的，因为不平滑的路径必然不会成为最佳路径——这实际上排除了大量弯弯绕绕的路径。总结下来也就是说，上面的式子就是在最佳路径的周围增加了扰动曲线，为的就是使得这个已知的$y^{\ast }$路径用时小于所有周围的扰动路线。

$y^{\ast }(x)$和$\eta (x)$是相对固定的，这意味着每个$\epsilon$值都将决定一条特定的相邻路径$y(x)$，从而决定最开始那个泛函的特定值。很容易发现，当 $\epsilon \to 0$ 时，相邻的路径将无限接近最优路径，也就是$\epsilon$直接决定了路径是否达到最优，到这里我们可以把前面的泛函改回我们熟悉的关于$\epsilon$的函数，我们记为$I(\epsilon )$ 。

显然，在 $\epsilon =0$ 时，$I(\epsilon )$ 取到极值，用微积分的表达就是 $${\frac{dI}{d\epsilon }|}_{\epsilon =0}=0$$ 这实际上就是极值路径的一个定义性质，由此可知$\frac{dI}{d\epsilon }=0$ 是极值路径的一个必要条件。但是这个式子使用的是任意变量$\epsilon$和任意扰动函数$\eta (x)$，因此实际无法进行操作，接下来的工作就是利用这些思想来进行推导。

欧拉方程的推导

欧拉方程的成就，在于把前面不可操作的微分形式变得可操作。接下来的内容就是欧拉方程的推导。

回到泛函

根据定义，最优路径就是使得路径用时$T[y(x)]$最小的路径。任何路径必将经过某个$x$区间，因此路径的总值就是这些区间内路径的加总。根据微积分的思想，在连续时间情形下，$x_1$ 到 $x_2$ 区间的路径就是一个定积分。

在连续的路径上找到某个时刻的「路径」，我们需要三部分信息：开始阶段、开始状态、「路径」方向。由于每条「路径」都是无限小的，因此三部分信息可以表示为$x,y(x),y^{\prime }(x)$。如果存在某个函数$F$可以将这三个量转化为「路径」的值，那么某一路径$A$在某一时刻$x_0$的值可以写为$F[x_0,y_A(x_0),y_A^{\prime }(x_0)]$。所以整个泛函可以被改写为 $$T[y]={\int }_0^{x}F[x,y(x),y^{\prime }(x)]dx$$

从泛函到函数

有了上面的式子，加上前面对于可行路径的定义，前面的关于$\epsilon$的函数$I(\epsilon )$ 就可以写为 $$I(\epsilon )={\int }_0^{X}F[x,y^{\ast }+\epsilon \eta ,y^{\ast \prime }+\epsilon {\eta }^{\prime }]dx$$ 为了简化表达，这里将函数写成了变量。

我们最终的目标是 $${\frac{dI}{d\epsilon }|}_{\epsilon =0}=0$$ 被积的变量是 $x$，根据莱布尼兹法则，我们可以穿过积分符号对$\epsilon$进行求导。 $$\frac{dI}{d\epsilon }={\int }_0^X\frac{dF}{d\epsilon }dx\text{\hspace{1em}(2.4.1)}$$

全微分

为了简化过程，我们令$$u=y^{\ast }+\epsilon \eta v=y^{\ast \prime }+\epsilon {\eta }^{\prime }$$ 被积函数即为$F(x,u,v)$，根据全微分公式有 $$\frac{\partial F}{\partial \epsilon }=\frac{\partial F}{\partial x}\cdot \frac{\partial x}{\partial \epsilon }+\frac{\partial F}{\partial u}\cdot \frac{\partial u}{\partial \epsilon }+\frac{\partial F}{\partial v}\cdot \frac{\partial v}{\partial \epsilon }$$ 显然，第一项为 0，后两项又有 $$\frac{\partial u}{\partial \epsilon }=\eta \frac{\partial v}{\partial \epsilon }={\eta }^{\prime }$$ 因此 $$\frac{\partial F}{\partial \epsilon }=\frac{\partial F}{\partial u}\cdot \eta +\frac{\partial F}{\partial v}\cdot {\eta }^{\prime }$$ (2.4.1)变为 $$\frac{dI}{d\epsilon }={\int }_0^X(\frac{\partial F}{\partial u}\cdot \eta +\frac{\partial F}{\partial v}\cdot {\eta }^{\prime })dx\text{\hspace{1em}(2.4.2)}$$

极值点

现在让$ϵ=0$，注意到，此时$u=y^{\ast },v=y^{\ast \prime }$，所以 $${\frac{dI}{d\epsilon }|}_{\epsilon =0}={\int }_0^X(\frac{\partial F}{\partial y^{\ast }}\cdot \eta +\frac{\partial F}{\partial y^{\ast \prime }}\cdot {\eta }^{\prime })dx=0$$ 利用积分的性质，被积函数第一项暂且不看，先看第二项，注意$\eta$是关于$x$的函数，所以可以写为 $${\int }_0^x\frac{\partial F}{\partial y^{\ast \prime }}\cdot \frac{\partial \eta }{\partial x}dx={\int }_0^x\frac{\partial F}{\partial y^{\ast \prime }}d\eta$$ 这时候就可以使用分部积分法$\int udv=uv-\int vdu$求积分。 $${\int }_0^X\frac{\partial F}{\partial y^{\ast \prime }}d\eta ={\eta \frac{\partial F}{\partial y^{\ast \prime }}|}_0^X-{\int }_0^X\eta \frac{\partial }{dx}(\frac{\partial F}{\partial y^{\ast \prime }})$$ 由于$\eta (x)$和最优路径有相同的起点和终点，因此第一项显然为 0。代回原式可得： $${\frac{dI}{d\epsilon }|}_{\epsilon =0}={\int }_0^X(\frac{\partial F}{\partial y^{\ast }}\cdot \eta -\eta \frac{\partial F_{y^{\ast \prime }}}{dx})dx={\int }_0^X\eta [\frac{\partial F}{\partial y^{\ast }}-\frac{\partial F_{y^{\ast \prime }}}{dx}]=0$$ 现在我们可以使用 2.2 中的定理了。要使得这个微分结果为0，这意味着有 $$F_{y^{\ast }}-\frac{\partial }{dx}{F}_{y^{\ast \prime }}=0t\in [x_1,x_2]$$

这就是欧拉方程（Euler equation），它就是极值路径的一个必要条件。

另一种形式的欧拉方程

现在对$F(x,y,y^{\prime })$做$x$的全微分： $$\frac{\partial F}{\partial x}=\frac{\partial F}{\partial x}\cdot \frac{\partial x}{\partial x}+\frac{\partial F}{\partial y}\cdot \frac{\partial y}{\partial x}+\frac{\partial F}{\partial y^{\prime }}\cdot \frac{\partial y^{\prime }}{\partial x}=\frac{\partial F}{\partial x}+\frac{\partial F}{\partial y}\cdot y^{\prime }+\frac{\partial F}{\partial y^{\prime }}\cdot y^{\prime \prime }$$

考虑这样一个函数的微分 $$\frac{\partial }{\partial x}\left(y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }}\right)=y^{\prime \prime }\frac{\partial F}{\partial y^{\prime }}+y^{\prime }\cdot \frac{\partial }{\partial x}(\frac{\partial F}{\partial y^{\prime }})$$ 由全微分可推知 $$\frac{\partial F}{\partial y^{\prime }}\cdot y^{\prime \prime }=\frac{\partial F}{\partial x}-\frac{\partial F}{\partial x}-\frac{\partial F}{\partial y}\cdot y^{\prime }$$ 将其代入得 $$\frac{\partial }{\partial x}\left(y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }}\right)=\left(\frac{\partial F}{\partial x}-\frac{\partial F}{\partial x}-\frac{\partial F}{\partial y}\cdot y^{\prime }\right)+y^{\prime }\cdot \frac{\partial }{\partial x}(\frac{\partial F}{\partial y^{\prime }})$$ 拆括号化简可得 $$\frac{\partial }{\partial x}\left(y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }}\right)=\frac{\partial F}{\partial x}-\frac{\partial F}{\partial x}+y^{\prime }\left[\frac{\partial F}{\partial y}-\frac{\partial }{\partial x}(\frac{\partial F}{\partial y^{\prime }})\right]$$ $\left[\frac{\partial F}{\partial y}-\frac{\partial }{\partial x}(\frac{\partial F}{\partial y^{\prime }})\right]$实际上就是上面所推导出的欧拉方程，在最优路径上其值为 0，因此该式可化为 $$\frac{\partial F}{\partial x}-\frac{\partial }{\partial x}(F-y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }})=0$$ 这就是另一种欧拉方程的形式。在某些情况下若能给定$\frac{\partial F}{\partial x}=0$，这意味着$x$并不显含于$F$（也就是$F(x,y,y^{\prime })$实际可能是$F(y,y^{\prime })$，$x$ 仍隐含于$F$），所有其他项在关于$x$偏微分时都视为常数，也就是说$F-y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }}$是一个常数$c$。 $$F-y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }}=C$$

最速曲线问题的解答

回到最开始的问题，我们已知 $$T={\int }_0^X\frac{\sqrt{1+y^{\prime 2}}}{\sqrt{2gy}}dx$$ 注意到$x$并不显含于$F$，因此可以用前面的欧拉方程的另一种形式 $$F-y^{\prime }\cdot \frac{\partial F}{\partial y^{\prime }}=C$$ 有 $$\frac{\partial F}{\partial y^{\prime }}=(2gy{)}^{-\frac{1}{2}}(1+y^{\prime 2}{)}^{-\frac{1}{2}}{y}^{\prime }$$ 代入欧拉方程 $$\frac{\sqrt{1+y^{\prime 2}}}{\sqrt{2gy}}-\frac{y^{\prime 2}}{\sqrt{2gy}\sqrt{1+y^{\prime 2}}}=C$$ 合并移项得 $$(1+(\frac{dy}{dx}{)}^2)y=\frac{1}{2g{C}^2}$$ 注意$\frac{1}{2g{C}^2}$是一个常数，我们令其为$k$ $$(\frac{dy}{dx}{)}^2=\frac{k-y}{y}$$ 所以 $$\sqrt{\frac{y}{k-y}}dy=dx$$ 注意到 $$\sqrt{\frac{y}{k-y}}=\sqrt{\frac{y/k}{1-\frac{y}{k}}}$$ 令$y/k=w$那么 $$\sqrt{\frac{y}{k-y}}=\sqrt{\frac{w}{1-w}}$$ 此时可以令$w=\frac{1}{2}(1-\cos \theta )$，因此 $$\sqrt{\frac{y}{k-y}}=\sqrt{\frac{\frac{1}{2}(1-\cos \theta )}{\frac{1}{2}(1+\cos \theta )}}=\frac{1-\cos \theta }{\sin \theta }$$ 所以可以进行换元，令$y=\frac{k}{2}(1-\cos \theta )dy=\frac{k}{2}\sin \theta d\theta$

所以 $$\sqrt{\frac{y}{k-y}}dy=\sqrt{\frac{1-\cos \theta }{1+\cos \theta }}\sqrt{\frac{1-\cos \theta }{1-\cos \theta }}\cdot \frac{k}{2}\sin \theta d\theta =dx$$ 化简得 $$\frac{k}{2}(1-\cos \theta )d\theta =dx$$ 对两边积分即可解出方程，得 $$x=\frac{k}{2}(\theta -\sin \theta )+C^{\prime }$$ 又已知$y_0=x_0=0$（过原点），因此可得最终的参数方程解 $$\{\begin{array}{rl}y& =\frac{k}{2}(1-\cos \theta )\\ x& =\frac{k}{2}(\theta -\sin \theta )\end{array}$$