变分法的思想
回到前面的问题:
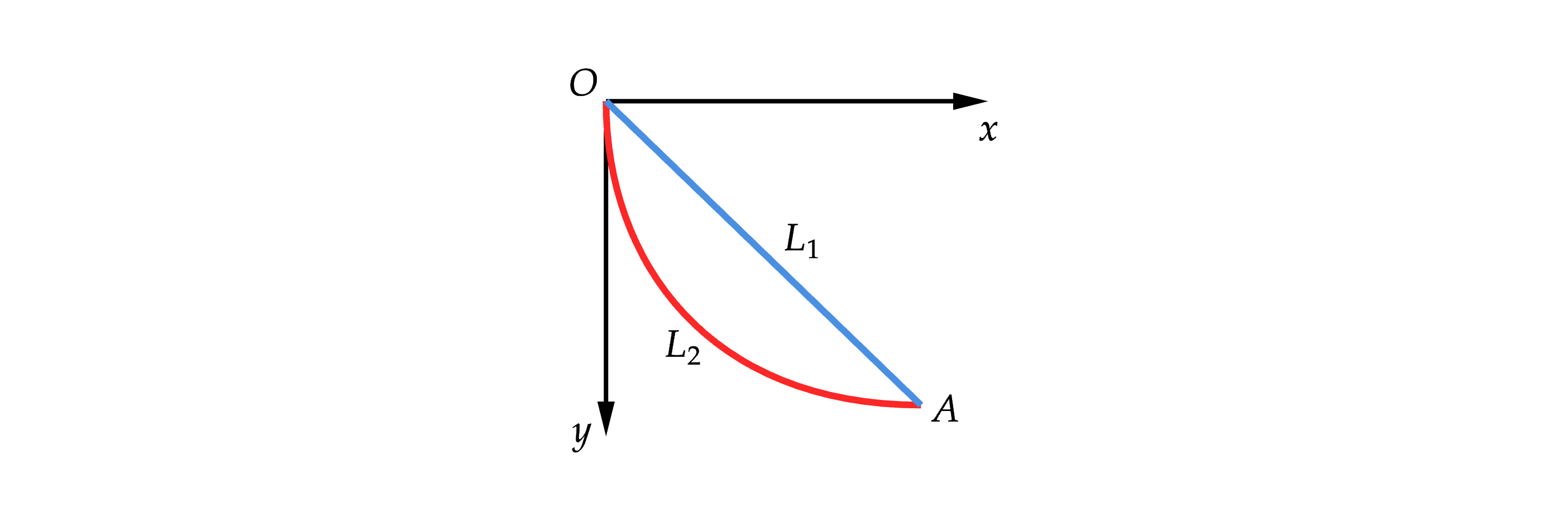 虽然我们暂时无法得知最佳路径的具体表达,但我们至少可以知道这条曲线本身是存在的,我们记为,而我们的目的,则是在众多的可能的路径中找到这个最优路径。我们可以这样表示一条与最佳路径相邻的,同样可以从 O 运动到 A 的可能路径:
其中,是一个常数,是一条路径,因为其同样可以从 O 运动到 A ,所以满足。此外, 必须是平滑的,因为不平滑的路径必然不会成为最佳路径——这实际上排除了大量弯弯绕绕的路径。总结下来也就是说,上面的式子就是在最佳路径的周围增加了扰动曲线,为的就是使得这个已知的路径用时小于所有周围的扰动路线。
虽然我们暂时无法得知最佳路径的具体表达,但我们至少可以知道这条曲线本身是存在的,我们记为,而我们的目的,则是在众多的可能的路径中找到这个最优路径。我们可以这样表示一条与最佳路径相邻的,同样可以从 O 运动到 A 的可能路径:
其中,是一个常数,是一条路径,因为其同样可以从 O 运动到 A ,所以满足。此外, 必须是平滑的,因为不平滑的路径必然不会成为最佳路径——这实际上排除了大量弯弯绕绕的路径。总结下来也就是说,上面的式子就是在最佳路径的周围增加了扰动曲线,为的就是使得这个已知的路径用时小于所有周围的扰动路线。
note
何为「变分」? 使得最终用时改变的,是不同路径的选择。「变分」指的就是在扰动路径进行微小变化后,观察泛函结果变化的过程。
和是相对固定的,这意味着每个值都将决定一条特定的相邻路径,从而决定最开始那个泛函的特定值。很容易发现,当 时,相邻的路径将无限接近最优路径,也就是直接决定了路径是否达到最优,到这里我们可以把前面的泛函改回我们熟悉的关于的函数,我们记为 。
显然,在 时, 取到极值,用微积分的表达就是 这实际上就是极值路径的一个定义性质,由此可知 是极值路径的一个必要条件。但是这个式子使用的是任意变量和任意扰动函数,因此实际无法进行操作,接下来的工作就是利用这些思想来进行推导。