动态最优化的性质

何为「动态」？

让我们先弄清楚什么是静态问题。某一时刻一家企业的利润函数为 $\pi (x)=F_x(Q)$。现需要求企业最大利润时的产量，很显然方法是求一阶导并令其为0。

通常来说该问题只有一个解，因为这只是在某一时刻下的选择。如果问题的解只是由每个选择变量的单个最优值组成的，这实际上就是静态优化问题。

而动态最优化涉及的问题通常为在计划期间的每个时段（离散时间情形）上或给定时间区间⽐如 $[0，T]$中的每个时点上，选择变量的最优值是多少。也就是说对于每个选择变量，你要给出它在今天的最优值、明天的最优值……直⾄计划期结束时的最优值。

最速曲线问题

在基础数学中，「两点之间线段最短」是一个非常基础的常识，但在物理学中却不尽然。

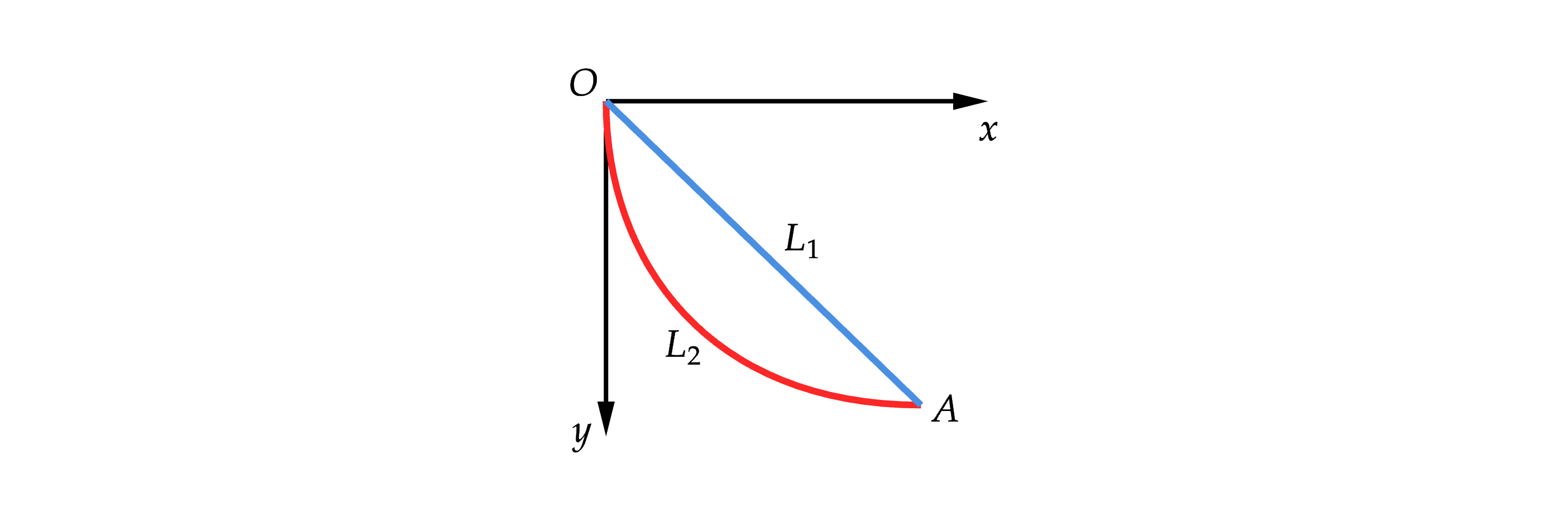
如上图，一个物体从 O 移动到 A 点，在数学几何意义上$L_1$是最短距离，但这并不意味着速度最快，实际上存在另一条路径$L_2$，沿着$L_2$从 O 移动到 A 点的用时最短。我们暂时不关心$L_2$具体的解，而是先看看求解的思考过程。

根据机械能守恒定理，满足 $$mgy=\frac{1}{2}m{v}^2$$ 其中$mgy$是重力势能，$\frac{1}{2}m{v}^2$为动能。由此可以解出 $$v=\sqrt{2gy}$$ 假设在某一时刻物体经过的路线长度为$s$，根据勾股定理有 $$ds=\sqrt{d{x}^2+d{y}^2}=dx\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}$$ 某一点的速度等于路程除以时间，那么就有 $$v=\frac{ds}{dt}⟹dt=\frac{ds}{v}$$ 两边同时积分，$dt$的积分即为在整段从 O 移动到 A 点所用的时间，令其为$T$，右边改为对 $x$ 积分。 $$\begin{array}{rl}\int dt=& \int \frac{ds}{v}\\ T=& \int \frac{\sqrt{d{x}^2+d{y}^2}}{\sqrt{2gy}}\\ T=& \int \frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}{\sqrt{2gy}}dx\end{array}$$ 要想求出最快的运动路径，实际就是让$T$最小。但需要注意的是，我们需要求的是「路径」，而不是一个「点」，而「路径」本身其实又是一个函数。我们知道，函数是一种从一个值映射到另一个值，而这里的 $T$ 却是从一个函数映射到另一个值。

这就是它的特别之处，一种路径到值的映射，这类映射有一个特别的名字：泛函（Functional）。接下来关于动态最优化的一个重要方法——变分法（Calculus of variations），其起点就是这里的泛函。